watches the people with basic math skills fight to the death over the answer
There’s quite a few calculators that get this wrong. In college, I found out that Casio calculators do things the right way, are affordable, and readily available. I stuck with it through the rest of my classes.
Ditto for Sharp. It’s really only Texas Instruments that is the ongoing exception to the rule.
Sharp as well.
My Casio calculators get this wrong, even the newer ones. BTW the correct answer is 16, right?
the correct answer is 16, right?
Yes
8 / 2 (2+2)
8 / 2 (4)
4 (4)
16
No
8 / 2 (2+2)
8 / 2 (4)
8 / 8
1
No. Order of operations is left to right, not right to left. 1 is wrong.
Order of operations is left to right
Order of operations is BEDMAS, THEN left to right within each operator.
1 is wrong
1 is the only correct answer.
Pemdas.
Multiplication comes before division.
1 is the correct answer.
1 is the correct answer, but it’s because Brackets comes before Division - there is no Multiplication in this problem.
That’s wrong. Multiplication and division have equal precedence, same as addition and subtraction. You do them left to right. PEMDAS could be rewritten like PE(MD)(AS). After parentheses and exponents, it"s Multiplication and division together, then addition and subtraction together. They also teach BODMAS some places, which is “brackets, order, division and multiplication, addition and subtraction” Despite reversing the division and multiplication, it doesn’t change the order of operations. They have the same priority, so they are just done left to right. PEMDAS and BODMAS are the different shorthand for the same order of operations.
There’s an argument to be made that implicit multiplication comes before division, resulting in the answer 1, but all multiplication? That’s wrong, full-stop. You calculate (explicit) multiplication and division in one step, left to right. Reason being that division is technically just multiplying by the reciprocal.
Yes
No.
8 / 2 (4) 8/(2x4) 8/8 1
deleted by creator
No, 8 / 2 happens before 2 * 4
That’s (2x4). Doing division before brackets goes against the order of operations rules.
deleted by creator
Division and multiplication are equal in the order of operations
I didn’t say they weren’t. I said…
Doing division before brackets goes against the order of operations rules
You did 8/2x4, which is the same as (8/2)(2+2), which isn’t the same as 8/2(2+2)=8/2(4)=8/(2x4).
Depends on the system you use. Most common system worldwide and in the academic circles (the oldest of the two) has 1 as the answer.
Depends on the system you use
There are no other systems - only people who are following the actual rules of Maths and those who aren’t. And yes, 1 is the correct answer
- 16 is the right answer if you use PEMDAS only:
(8 ÷ 2) × (2 + 2) - 1 is the right answer if you use implicit/explicit with PEMDAS:
8 ÷ (2 × (2 + 2)) - both are correct answers (as in if you don’t put in extra parentheses to reduce ambiguity, you should expect expect either answer)
- this is also one of the reasons why postfix and prefix notations have an advantage over infix notation
- postfix (HP, RPN, Forth):
2 2 + 8 2 ÷ × . - prefix (Lisp):
(× (÷ 8 2) (+ 2 2))
- postfix (HP, RPN, Forth):
16 is the right answer if you use PEMDAS only: (8 ÷ 2) × (2 + 2)
You added brackets and changed the answer. 2(2+2) is a single term, and if you break it up then you change the answer (because now the (2+2) is in the numerator instead of in the denominator).
1 is the right answer
The only right answer
both are correct answers
Nope, 1 is the only correct answer.
this is also one of the reasons why postfix and prefix notations have an advantage over infix notation
Except they don’t. This isn’t a notation problem, it’s a people don’t remember the rules of Maths problem.
prefix notation doesn’t need parentheses either though, at least in this case. lisp uses them for readability and to get multiple arity operators. infix doesn’t have any ambiguity either if you parenthesize all operations like that.
infix doesn’t have any ambiguity either if you parenthesize all operations like that
There isn’t any ambiguity even if you don’t.
- 16 is the right answer if you use PEMDAS only:
For anyone like me who has math as their worst subject: PEMDAS.
PEMDAS is an acronym used to mention the order of operations to be followed while solving expressions having multiple operations. PEMDAS stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.
So we gotta do it in the proper order. And remember, if the number is written like
2(3)then its multiplication, as if it was written2 x 3or2 * 3.So we read
8/2(2+2)and need to do the following;- Read the Parentheses of
(2 + 2)and follow the order of operations within them, which gets us 4. - Then we do
2(4)which is the same as2 x 4which is8 8 / 8is1.
The answer is 1. The old calculator is correct, the phone app which has ads backed into it for a thing that all computers were invented to do is inaccurate.
Turns out I’m wrong, but I haven’t been told how or why. I’m willing to learn if people actually tell me
Well, I don’t know what you said originally, so I don’t know what it is you were told was wrong - 1 or 16? 😂 The correct answer is 1.
Anyhow, I have an order of operations thread which covers literally everything there is to know about it (including covering all the common mistakes and false claims made by some). It includes textbook references, historical Maths documents, worked examples, proofs, memes, the works! I’m a high school Maths teacher/tutor - I’ve taught this topic many times.
not to be That Guy, but the phone is actually correct… multiplication and division have the same precedence, so
8 / 2 * 4should give the same result as8 * 4 / 2, ie 16but the phone is actually correct
No, it’s actually wrong.
8 / 2 * 4
It’s 8/(2x4). You can’t remove brackets unless there is only 1 term left inside.
Removed by mod
Me searching the place for my old Ti83 after stumbling on this thread.
My partner: why are you even looking for this thing??
Me: Somebody on the Internet is WRONG.
My partner: Good enough, I’ll help!
Except TI calculators also give the wrong answer when a bracketed term has a coefficient.
Then I admit I’m wrong, I just don’t get how PEMDAS/I got it wrong.
Short story, PEMDAS kinda sucks, because it has 4 levels of priority, but 6 letters:
- P
- E
- MD
- AS
M and D are the same level, priority is from left to right.
A and S are the same level, priority is from left to right.Just tested this on a Ti-83 too.
8/2(2+2) = 16

TI calculators disobey The Distributive Law and give the wrong answer when a bracketed term has a coefficient.
My one big criticism of the Ti-83/84 is implicit multiplication. Ti says 1/2x is 0.5x when I needed the reciprocal of 2x.
Yeah, that’s exactly the problem with TI calculators - ignoring the rules of Maths.
My calculator gets 1. Weird.
My calculator gets 1
That is the correct answer.
I thank you for proving me right, but this a 4 month old thread. Not complaining, just giving you a heads up.
this a 4 month old thread
Yeah, I know, but it’ll show up in search results for all eternity, and it’s full of disinformation. As a Maths teacher/tutor who is sick of hearing “But Google/Wolfram/TI says…”, I’m doing my best to try and get said people to fix their damn calculators (and also make people aware that those calculators are wrong. (sigh) I miss the old days when all calculators gave the right answer - what happened??). If you feel the same way then feel free to share my links - that’s what they’re there for. :-)
And right at the moment I’m feeling too tired to do anything which requires me to think about it, so just doing what I can do on automatic. ;-)
And also if I hadn’t been replying to this thread then you wouldn’t have got the proof that you were right. :-)
Well that’s just wrong… Multiplication and division have equal priorities so they are done from left to right. So: 8 / 2 * (2 + 2)=8 / 2 * 4=4 * 4=16
Implicit multiplication takes priority over explicit multiplication or division. 2(2+2) is not the same thing as 2*(2+2).
Correct! 2(2+2) is a single term - subject to The Distributive Law - and 2x(2+2) is 2 terms. Those who added a multiply sign there have effectively flipped the (2+2) from being in the denominator to being in the numerator, hence the wrong answer.
But it’s not called “implicit multiplication” - it’s Terms and/or The Distributive Law which applies (and they’re 2 separate rules, so you cannot lump them together as a single rule).
8 / 2 * (2 + 2)
That’s not the same as 8 / 2 (2 + 2). In the original question, 2(2+2) is a single term in the denominator, when you added the multiply you separated it and thus flipped the (2+2) to be in the numerator, hence the wrong answer.
Not quite, pemdas can go either from the left or right (as long as you are consistent) and division is the same priority as multiplication because dividing by something is equal to multiplying by the inverse of that thing… same as subtraction being just addition but you flip the sign.
8×1/2=8/2 1-1=1+(-1)
The result is 16 if you rewrite the problem with this in mind: 8÷2(2+2)=8×(1/2)×(2+2)
8÷2(2+2)=8×(1/2)×(2+2)
No, that’s wrong. 2(2+2) is a single term, and thus entirely in the denominator. When you separated the coefficient you flipped the (2+2) into the numerator, hence the wrong answer. You must never add multiplication signs where there are none.
I’ve never had anyone tell me operations with the same priority can be done either way, it’s always been left to right.
I’ve never had anyone tell me operations with the same priority can be done either way, it’s always been left to right
It’s left to right within each operator. You can do multiplication first and division next, or the other way around, as long as you do each operator left to right. Having said that, you also can do the whole group of equal precedence operators left to right - because you’re still preserving left to right for each of the two operators - so you can do multiplication and division left to right at the same time, because they have equal precedence.
Having said that, it’s an actual rule for division, but optional for the rest. The actual rule is you have to preserve left-associativity - i.e. a number is associated with the sign to the left of it - and going left to right is an easy way to do that.
I’ve always heard it that way too but I think it is for consistency with students, imo Logically, if you are looking at division = multiplying by inverse and subtraction = adding the negative, you should be able to do it both ways. Addition and multiplication are both associative, so we can do 1+2+3 = (1+2)+3 = 1+(2+3) and get the same answer.
But subtraction and division are not associative. Any time you work on paper, 2 - 2 - 2 would equal -2. That is, (2-2)-2=0-2=-2. If you evaluate right to left, you get 2-2-2=2-(2-2)=2-0=2
2-(2-2)
But you broke the rule of left-associativity there. You can go right to left provided you keep each number with the sign to it’s left (and you didn’t do that when you separated the first 2 in brackets from it’s minus sign).
Correct, subtraction and division are not associative. However, what is subtraction if not adding the opposite of a number? Or division if not multiplying the inverse? And addition and multiplication are associative.
2-2-2 can be written as 2 + (-2) + (-2) which would equal -2 no matter if you solve left to right, or right to left.
In your example with the formula from right to left, distributing the negative sign reveals that the base equation was changed, so it makes sense that you saw a different answer.
2 - (2 - 2) = 2 + ((-2) + 2) = 2
PEMDAS evaluated from left to right. If you followed that you’d get 16. 1 is ignoring left to right.
1 isn’t ignoring anything. 16 can be arrived at by ignoring any one of multiple order of operations rules.
Uh… no the 1 is wrong? Division and multiplication have the same precedence, so the correct order is to evaluate from left to right, resulting in 16.
There’s no multiplication in this question - multiplication refers literally to multiplication signs - only division and brackets, and addition within the brackets. So you have to use The Distributive Law to solve the brackets, then do the division, giving you 1.
The problem is that the way PEMDAS is usually taught multiplication and division are supposed to have equal precedence. The acronym makes it look like multiplication comes before division, but you’re supposed to read MD and as one step. (The same goes for addition and subtraction so AS is also supposed to be one step.) It this example the division is left of the multiplication so because they have equal precedence (according to PEMDAS) the division applies first.
IMO it’s bad acronym design. It would be easier if multiplication did come before division because that is how everyone intuitively reads the acronym.
Maybe it should be PE(M/D)(A/S). But that version is tricky to pronounce. Or maybe there shouldn’t be an acronym at all.
but you’re supposed to read MD and as one step
You can do them in any order at all - M then D, D then M (hence the acronym BEDMAS), or all in one - what does matter is not treating Distribution as though it’s Multiplication (which refers literally to multiplication signs), when in actual fact it’s the first step in solving Brackets.
The problem with this is that the division symbol is not an accurate representation of the intended meaning. Division is usually written in fractions which has an implied set of parenthesis, and is the same priority as multiplication. This is because dividing by a number is the same as multiplying by the inverse, same as subtracting is adding the negative of a number.
8/2(2+2) could be rewritten as 8×1/2×(2+2) or (8×(2+2))/2 which both resolve into 16.
You left out the way it can be rewritten which most mathematicians would actually use, which is 8/(2(2+2)), which resolves to 1.
Division is usually written in fractions
Division and fractions aren’t the same thing.
fractions which has an implied set of parenthesis
Fractions are explicitly Terms. Terms are separated by operators (such as division) and joined by grouping symbols (such as a fraction bar), so 1÷2 is 2 terms, but ½ is 1 term.
8/2(2+2) could be rewritten as 8×1/2×(2+2)
No, it can’t. 2(2+2) is 1 term, in the denominator. When you added the multiply you broke it into 2 terms, and sent the (2+2) into the numerator, thus leading to a different answer. 8/2(2+2)=1.
- Read the Parentheses of
Different compilers have robbed me of all trust in order-of-operations. If there’s any possibility of ambiguity - it’s going in parentheses. If something’s fucky and I can’t tell where, well, better parenthesize my equations, just in case.
Different compilers
Different programmers.
it’s going in parentheses
Unfortunately some places don’t care where you’ve put brackets, they’ll just go ahead and change it anyway. Welcome to my quest to educate.
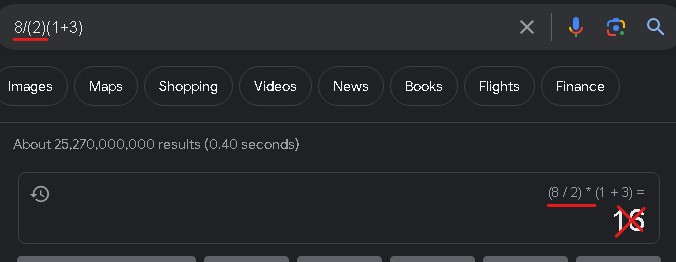
That’s the same ambiguity, numbnuts. Your added parentheses do nothing. If you wanted to express the value 8 over the value 2*(1+3), you should write 8/(2*(1+3)). That is how you eliminate other valid interpretations.
As illustration of why there are competing valid interpretations: what human being is going to read “8/2 * (1+3)” as anything but 4*4? Those spaces create semantic separation. But obviously most calculators don’t have a spacebar, any more than they have to ability to draw a big horizontal line and place 2(1+3) underneath it. Ambiguous syntax for expressing mathematics is not some foundation-shaking contradiction. It’s a consequence of limitations in how we express even the most concrete ideas.
“The rules of math” you keep spamming about are not mathematical proofs - they’re arbitrary decisions made by individuals and organizations. In many cases the opposite choice would be equally sensible. Unlike the innate equivalence of multiplication and division, where dividing by two and multiplying by half are interchangeable. Same with addition and subtraction.
Do you want to argue that 8 - (2) + (1+3) should be 2?
Your added parentheses do nothing
So you’re saying Brackets aren’t first in order of operations? What do you think brackets are for?
If you wanted to express the value 8 over the value 2*(1+3), you should write 8/(2*(1+3))
or, more correctly 8/2(1+3), as per the rules of Maths (we never write unnecessary brackets).
That is how you eliminate other valid interpretations
There aren’t any other valid interpretations. #MathsIsNeverAmbiguous
what human being is going to read “8/2 * (1+3)” as anything but 4*4
Yes, that’s right, but 8/2x(1+3) isn’t the same as 8/2(1+3). That’s the mistake that a lot of people make - disobeying The Distributive Law.
Those spaces
…have no meaning in Maths. The thing that separates the Terms, in your example, is the multiply. i.e. an operator.
most calculators don’t have a spacebar
…because it’s literally meaningless in Maths.
any more than they have to ability to draw a big horizontal line and place 2(1+3) underneath it
Some of them can actually.
“The rules of math” you keep spamming about are not mathematical proofs
You should’ve read further on then. Here’s the proof.
they’re arbitrary decisions made by individuals
No, they’re a natural consequence of the way we have defined operators. e.g. 2x3=2+2+2, therefore we have to do multiplication before addition.
In many cases the opposite choice would be equally sensible
2+2x3=2+6=8 the correct answer, but if I do addition first…
2+2x3=4x3=12, which is the wrong answer. How is getting the wrong answer “equally sensible” as getting the right answer?
Do you want to argue that 8 - (2) + (1+3) should be 2?
No, why would I do that? 8-(2+1+3) does equal 2 though.
You are a smug idiot.
8/2(1+3) is exactly the sort of thing programs love to misinterpret. I don’t give a shit what “rules of math” you insist are super duper universal, or what “we” do. They are not reliable. Clear parentheses are. Insisting you’re correct is not relevant. You stumbled into a pragmatic issue with grand philosophical assurances that aren’t even sound.
Yes, that’s right, but 8/2x(1+3) isn’t the same as 8/2(1+3).
… no, that’s fucking stupid.
Some of them can actually.
Hence the word “most.” Your cocksure months-late manic episode across this thread is the most “akshually” thing I have ever witnessed.
Here’s the proof.
You dense bastard! That’s a category error! You can’t prove that 2(3) means something different from 2*3. It’s only convention! It’s a thing we made up, unlike actual mathematical proofs, which are laws of the universe. If everyone disagreed with that then it would stop being true. That’s not a sentence you can say about anything that has a proof, instead of some evidence.
You keep talking about “rules of math” when what you mean is rules of this particular notation. Reverse Polish Notation doesn’t have this issue, at all. Distribution is not even possible in RPN. So however important you think it might be… it’s not universal.
[Those spaces] have no meaning in Maths.
THAT’S THE POINT, NUMBNUTS. It’s semantic separation that human beings will read in for context. Which they need, because some grammars have ambiguities, which can only be resolved by convention. Like how -6 is a number, and you can add or multiply -6, but 1 + -6 looks kinda weird, -6(3) is fine, and (3) -6 is asking for trouble.
The convention overwhelmingly used in computation is that parentheses are resolved first. Nothing is distributed over them - they are evaluated, and then used. In exactly the same way that multiplication can be treated as repeated addition, operations on parentheticals are treated as operations on equations reduced to scalars. It doesn’t fucking mean anything, to say 8/2*(1+3) is different from 8/2(1+3), because in the notation used by coders, they both become 8/2*4.
You might as well barge in pick a fight with N=N+1.
You are a smug idiot
That’s your colloquialism for Maths teachers. Ok, got it.
8/2(1+3) is exactly the sort of thing programs love to misinterpret.
Programs, written by programmers, who have forgotten the rules of Maths.
that’s fucking stupid
So you’re saying the rules of Maths are stupid. Got it.
You can’t prove that 2(3) means something different from 2*3. It’s only convention!
No, it’s a rule of Maths - it’s literally the opposite operation to factorising.
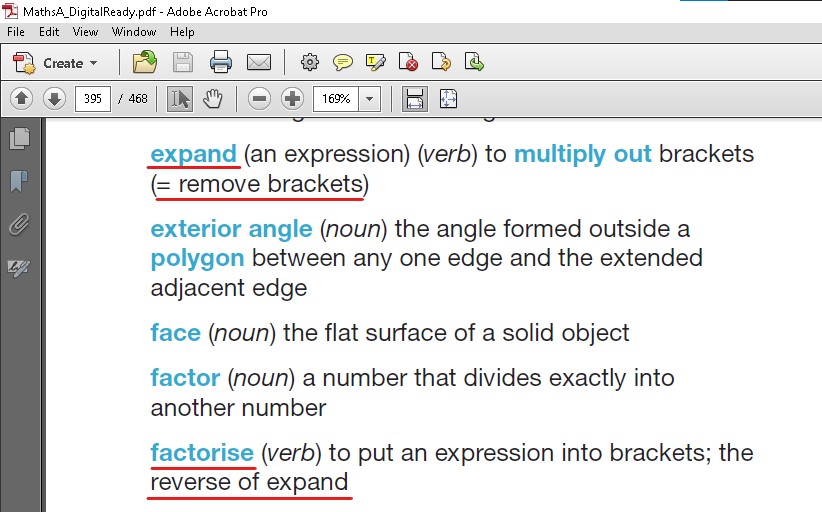
It’s a thing we made up
Nothing in Maths is made up. It’s based on our observations of how things work.
mathematical proofs, which are laws of the universe
Now you’re getting it.
this particular notation
…which is Maths.
Reverse Polish Notation doesn’t have this issue, at all
Neither does infix notation. All notations have to obey the rules of Maths, since the rules of Maths are universal.
Distribution is not even possible in RPN
Second hit in my Google results…

(3) -6 is asking for trouble
It’s -3 - where’s the trouble?
say 8/2*(1+3) is different from 8/2(1+3), because in the notation used by coders, they both become 8/2*4
Welcome to why almost every single e-calculator is wrong (as opposed to handheld calculators) - MathGPT gets it right.
Nothing in Maths is made up. It’s based on our observations of how things work.
The notation and syntax of how we express that, is made-up. There’s multiple options. There’s disagreements. Fuck me sideways, you are a teacher, and you can’t figure out how being off-topic works?
Evidently not, as you flip between ‘this particular notation is the notation!’ to ‘of course other notations exist’ and suffer zero cognitive dissonance. By capital-M “Maths,” do you mean the notation on paper, or the underlying laws-of-reality stuff? It depends! It’s ambiguous and requires context, or maybe you’re just factually wrong at least one of those times, and either way, that means it’s plainly not THE SAME KIND OF THING as the laws-of-reality stuff.
It’s a category error. You can prove that the word prove isn’t spelled proove, for some reason, but the heavens would not bend the other direction if that changed. We could swap square braces and parenthesis and nothing would be different. We could use the glyph “&” instead of “7.” These details are mutable and completely fucking arbitrary. But then & - 6 = 1, and you could never proove otherwise.
Second hit in my Google results…
Shows B being subtracted from A before that value is multiplied by C. It’s not distribution. It’s evaluating the parenthetical.
It’s -3 - where’s the trouble?
The fact it’s 3 and -6, not 3 - 6. Which is why I explicitly mentioned that -6 was a number, and used two other examples with -6. I wasn’t just making conversation. Jesus fucking Christ, a state trusts you with the education of children.
According to the textbook you’re now screenshotting at people, A(B) and (B)A are both correct - yes? They’re both valid? And spaces have no impact on an equation? And writing equations like -6 + 1 are fine, instead of (-6) + 1, since you don’t want needless parentheses?
‘this particular notation is the notation!’ to ‘of course other notations exist’
The notation for division in some countries is the obelus, in other countries it’s a colon. Whatever country you’re in, the notation for that country is the notation for division (be it an obelus or a colon).
Maths,” do you mean the notation on paper, or the underlying laws-of-reality stuff
Both! Whatever notation your country uses, all the rules for Maths and use of that Maths notation are defined.
It’s ambiguous
No, it’s not.
It’s not distribution. It’s evaluating the parenthetical
And Distribution applies to brackets/parentheses where they have a coefficient. In other words, same same.
it’s 3 and -6, not 3 - 6
You didn’t put a comma between 3 and -6, so no, it’s not 3 and -6, it’s 3-6. That’s what you wrote, that’s what it is.
a state trusts you with the education of children
Related - have you noticed how children never get this wrong? It’s only adults who’ve forgotten the rules of Maths who get it wrong.
According to the textbook you’re now screenshotting at people, A(B) and (B)A are both correct - yes? They’re both valid? And spaces have no impact on an equation? And writing equations like -6 + 1 are fine, instead of (-6) + 1, since you don’t want needless parentheses?
Yes (though the latter is unconventional), yes (though the latter is unconventional), yes, yes (though unconventional - 1-6 is the conventional way to write that), yes, yes.
This is best practice since there is no standard order of operations across languages. It’s an easy place for bugs to sneak in, and it takes a non-insignificant amount of time to debug.
there is no standard order of operations across languages
Yes there is. The rules of Maths are universal.
It’s an easy place for bugs to sneak in
But that’s because of programmers not checking the rules of Maths first.
This is the way. It’s an intentionally ambiguously written problem to cause this issue depending on how and where you learned order of operations to cause a fight.
intentionally ambiguously written
#MathsIsNeverAmbiguous
learned order of operations to cause a fight
The order of operations are the same everywhere. The fights arise from people who don’t remember them.
Please see this section of Wikipedia on the order of operations.
The “math” itself might not be ambiguous, but how we write it down absolutely can be. This is why you don’t see actual mathematicians arguing over which one of these calculators is correct - it is not either calculator being wrong, it is a poorly constructed equation.
As for order of operations, they are “meant to be” the same everywhere, but they are taught differently. US - PEMDAS vs UK - BODMAS (notice division and multiplication swapped places). Now, they will say they are both given equal priority, but you can’t actually do all of the multiplication and division at one time. Some are taught to simply work left to right, while others are taught to do multiplication first; but we are all taught to use parentheses correctly to eliminate ambiguity.
Please see this section of Wikipedia on the order of operations
That section is about multiplication, and there isn’t any multiplication in this expression.
The “math” itself might not be ambiguous, but how we write it down absolutely can be
Not in this case it isn’t. It has been written in a way which obeys all the rules of Maths.
This is why you don’t see actual mathematicians arguing over which one of these calculators is correct
But I do! I see University lecturers - who have forgotten their high school Maths rules (which is where this topic is taught) - arguing about it.
it is not either calculator being wrong
Yes, it is. The app written by the programmer is ignoring The Distributive Law (most likely because the programmer has forgotten it and not bothered to check his Maths is correct first).
US - PEMDAS vs UK - BODMAS
Those aren’t the rules. They are mnemonics to help you remember the rules
notice division and multiplication swapped places
Yes, that’s right, because they have equal precedence and it literally doesn’t matter which way around you do them.
you can’t actually do all of the multiplication and division at one time
Yes, you can!
Some are taught to simply work left to right
Yes, that’s because that’s the easy way to obey the actual rule of Left associativity.
we are all taught to use parentheses correctly to eliminate ambiguity
Correct! So 2(2+2) unambiguously has to be done before the division.
Just out of curiosity, what is the first 2 doing in “2(2+2)”…? What are you doing with it? Possibly multiplying it with something else?
there isn’t any multiplication in this expression.
Interesting.
I really hope you aren’t actually a math teacher, because I feel bad for your students being taught so poorly by someone that barely has a middle school understanding of math. And for the record, I doubt anyone is going to accept links to your blog as proof that you are correct.
Just out of curiosity, what is the first 2 doing in “2(2+2)”…? What are you doing with it? Possibly multiplying it with something else?
Distributing it, as per The Distributive Law. Even Khan Academy makes sure to not call it “multiplication”, because that refers literally to multiplication signs., which, as I said, there aren’t any in this expression - only brackets and division (and addition within the brackets).

I feel bad for your students
My students are doing well thanks.

I doubt anyone is going to accept links to your blog as proof that you are correct
You mean the blog that has Maths text book references, historical Maths documents, and proofs? You know proofs are always true, right? But thanks for the ad hominem anyway, instead of any actual proof or evidence to support your own claims.
[…] the question is ambiguous. There is no right or wrong if there are different conflicting rules. The only ones who claim that there is one rule are the ones which are wrong!
https://people.math.harvard.edu/~knill/pedagogy/ambiguity/index.html
As youngsters, math students are drilled in a particular
convention for the “order of operations,” which dictates the order thus:
parentheses, exponents, multiplication and division (to be treated
on equal footing, with ties broken by working from left to right), and
addition and subtraction (likewise of equal priority, with ties similarly
broken). Strict adherence to this elementary PEMDAS convention, I argued,
leads to only one answer: 16.Nonetheless, many readers (including my editor), equally adherent to what
they regarded as the standard order of operations, strenuously insisted
the right answer was 1. What was going on? After reading through the
many comments on the article, I realized most of these respondents were
using a different (and more sophisticated) convention than the elementary
PEMDAS convention I had described in the article.In this more sophisticated convention, which is often used in
algebra, implicit multiplication is given higher priority than explicit
multiplication or explicit division, in which those operations are written
explicitly with symbols like x * / or ÷. Under this more sophisticated
convention, the implicit multiplication in 2(2 + 2) is given higher
priority than the explicit division in 8÷2(2 + 2). In other words,
2(2+2) should be evaluated first. Doing so yields 8÷2(2 + 2) = 8÷8 = 1.
By the same rule, many commenters argued that the expression 8 ÷ 2(4)
was not synonymous with 8÷2x4, because the parentheses demanded immediate
resolution, thus giving 8÷8 = 1 again.This convention is very reasonable, and I agree that the answer is 1
if we adhere to it. But it is not universally adopted.That’s cool, but still wrong :3
[…] the question is ambiguous. There is no right or wrong if there are different conflicting rules. The only ones who claim that there is one rule are the ones which are wrong!
https://people.math.harvard.edu/~knill/pedagogy/ambiguity/index.html
Yeah nah. Actual Maths textbooks and proofs - did you not notice the complete lack of references to textbooks in the blog? It’s funny that he mentions Cajori though, given Cajori has a direct reference to Terms #MathsIsNeverAmbiguous

I think I’m gonna trust someone from Harvard over your as-seen-on-TV looking ass account, but thanks for the entertainment you’ve provided by trying to argue with some of the actual mathematicians in here
I think I’m gonna trust someone from Harvard
So you’re going with the appeal to authority argument - ok, got it.
But if you’re gonna do that then make sure you check out Cajori’s credentials, since that’s, you know, who we both quoted.
argue with some of the actual mathematicians in here
You mean the dude who claimed to be, and was quoting wikipedia? BWAHAHAHAHA
Everyone in this threading referencing PEMDAS and still thinking the answer is 1 are completely ignoring the part of the convention is left to right. Only way to get 1 is to violate left to right on multiplication and division.
Only way to get 1 is to violate left to right on multiplication and division
Actually the only way to get 16 is to ignore one of more rules of Maths - sometimes it’s Terms, sometimes it’s The Distributive Law, but always something. If you follow all the rules of Maths you get 1.
The problem is that BIDMAS and its variants are lies-to-children. Real mathematicians don’t use BIDMAS. Multiplication by juxtaposition is extremely common, and always takes priority over division.
Nobody in their right minds would saw 1/2x is the same as (1/2)x. It’s 1/(2x).
That’s how you get 1. By following conventions used by mathematicians at any level higher than primary school education.
The problem is the /. Usually you’d use a fraction bar, which groups it and makes it unambiguous
Usually you’d use a fraction bar, which groups it and makes it unambiguous
Division (operator) and fraction bar (grouping symbol) aren’t the same. It already is unambiguous.
Source? I have a hard ass time believing that nobody in their right mind would do pemdas the way you’re supposed to do it xD
Source?
Cajori (1928) for starters, plus any old Year 7 Maths textbook, any era (we know from Lennes letter that textbooks were already doing this in 1917).

The problem is that you’re thinking of BIDMAS as a set of hard rules, rather than the set of rough guidelines created in the early 20th century by one random teacher for the purposes of teaching 10-year-olds how to do the level of maths that 10-year-olds do.
This video and this one point to some examples of style guides in academia as well as practical examples in the published works of mathematicians and physicists, which are pretty consistent.
If you want to come up with a hard rule, doing BIJMDAS, adding in “multiplication indicated by juxtaposition” with the J, is a much better way to do it than what you learnt when you were 10. But even that’s still best to think of as a handy guideline rather than a hard and fast rule.
That’s cool, but still wrong :3
No fr I had no idea that those acronyms weren’t the whole picture, I just assumed some mathematicians a long time ago decided how that stuff should be written out and that BEDMAS/PEMDAS/whatever contained all the rules in it. Thank you for the info, Idk why this isn’t more widely taught, ig because those acronyms are what all the questions are already written for? It doesn’t seem that hard to just teach it as BEADMAS, where the A refers to numbers adjacent to variables
It doesn’t seem that hard to just teach it as BEADMAS, where the A refers to numbers adjacent to variables
Terms already are taught!
I don’t understand why people say Maths. Math encompasses every single type of Math. Maths is just wrong.
I don’t understand why people say Maths
Because it’s plural.
every single type of Math
In other words, every branch of Mathematics.
It’s a shortened form of mathematics, build a bridge and get over it
Ok, but the British also shortened television and made it tele. That makes sense because they took part of the word to do it. If you were going to shorten the word mathematics, why wouldn’t it be math, especially when that would follow what you did with television. Why shorten the word and then add the s from the end for no reason?
why wouldn’t it be math, especially when that would follow what you did with television
Because television is singular (a TV set) and Maths is plural, same as Bros. is the abbreviation of brothers. i.e. when abbreviating a plural you keep the “s”.
Television isn’t a plural word tho? And if they were talking about more than one television I feel like they would absolutely say teles (tellies?), altho not British so 🤷♂️
What is math short for?
Because it’s British English
That may be, but Math still encompasses all Math so there’s no need to pluralize it.
Mathematics.
The discipline is “mathematics.” It’s really not unreasonable that in some parts of the world, it got shortened to maths.
And the other error present is the incorrect pluralisation. Mathematica means the entire area or domain of knowledge, while mathematics sounds like several lines of thinking, which is weird when we use it as a singular. Maths doesn’t refer to several kinds of math, and that’s confusing.
Mathematica
Maths doesn’t refer to several kinds of math
It refers to all branches of Mathematics.
That’s an after the fact justification.
That’s an after the fact justification
You got some sources with dates in them to show it was “after”, and not, you know, before?
And British English is wrong. Those motherfuckers stick “u” into way too many words.
I’ll have you find that there’s more Americans and statistically likely to have more “motherfuckers” in america
Anymore of this disrespect and I’ll stick “u” into an early grave.
/jk
I feel obligated to say English that comes from England is the only real English. You can keep your Americanese.
16
Please Excuse My Dear Aunt Sally, she downloaded a shitty ad-infested calculator from the Google Play store.
The calculator is correct
The problem is that there’s no “external” parentheses to really tell us which is right:
(8 / 2) * 4or8 / (2 * 4)The amount of comments here shows how much debate this “simple” thing generates
Afaik the order of operations doesn’t have distributive property in it. It would instead simply become multiplication and would go left to right and would therefore be 16.
Afaik the order of operations doesn’t have distributive property in it
The Distributive Law applies to all bracketed terms that have a coefficient. It’s literally the first step in solving brackets.
The problem is that there’s no “external” parentheses to really tell us which is right: (8 / 2) * 4 or 8 / (2 * 4)
The Distributive Law tells us it’s the latter.
If you agree that parenthesis go first then the equation becomes 8/2x4. Then it’s simply left to right because multiplication does not take precedence over division. What’s the nuanced talk? That M comes before D in PEMDAS?
If you agree that parenthesis go first then the equation becomes 8/2x4
No, it becomes 8/(2x4). You can’t remove brackets unless there’s only 1 term left inside. Removing them prematurely flips the 4 from being in the denominator to being in the numerator, hence the wrong answer.
Ah damn it. It took me ages to find a calculator app that fits my needs… And now I find out it works like the one on the right.
… the one on the right is correct… that’s a jank ass calculator on the left that doesn’t know how to do order of operations 8/2×(2+2) 8/2x4 4x4 16
the one on the right is correct
No, it isn’t.
8/2×(2+2)
…isn’t the same thing as 8/2(2+2). You separated the term in the denominator, leading the (2+2) to get flipped into the numerator, hence wrong answer.
That would be 8/(2x(2+2)) if we were keeping it all in the denominator. Multiplication happens in the numerator if there are no parenthesis to distinguish it. If thr equation was written like this:
8
2x(2+2)
Then you would also be correct, but I have to respectfully disagree with your analysis.
That would be 8/(2x(2+2)) if we were keeping it all in the denominator
(2x(2+2)) is the same thing as 2(2+2)
I have to respectfully disagree with your analysis
Which means you disagree with how Maths textbooks teach how to do this (see previous link).
There isn’t a multiplication symbol though. By your logic something like
8÷2xwould mean(8÷2)*xbecause order of operationsOr if you read
8÷2√xas(8÷2)*√xJust notate
8÷2(2+2)as8÷2x; x=(2+2)and you get it, you can substitute any complete expression with a variable in an equation and the logic stays the same.You know sometimes both are correct.
You know sometimes both are correct
Nope. That’s what the order of operations rules take care of.
Hiper Calc is the calculator app that I use. It’s very good. When I ran this equation, it actually notified me how the operands should be grouped (weak or strong) and provided two answers. Honestly the whole issue can be avoided if you use more parentheses
the whole issue can be avoided
…by following all the order of operations rules
this is why I never use ÷ (or more realistically “/”) without explicit brackets denoting order of operations.
So umm what’s the correct one?
what’s the correct one?
Yes, one is correct :-)
If you believe multiplication goes before division then
1.8 / (2 * 4)If you believe multiplication and division are of equal importance
16.8 / 2 * 4SQL, Google, and I believe C++ and HLSL would say the latter: (
16)If you believe multiplication goes before division then 1. 8 / (2 * 4)
That’s not “multiplication” though - that’s The Distributive Law. Multiplication refers literally to multiplication signs.
I don’t think you encounter this one very often, but the technically correct
-2^2 = -4has a higher chance of ruining your day.You mean x^2 =4 where x=±2
No, you’d expect that -2^2 would equal 4, but calculators solve it as -(2)^2 not (-2)^2. But the case you mentioned is also pretty common.
if you’ve touched polynomials ever, you’d expect the exponent to be before the negation. If you write x³-x² you don’t mean x³ + (-x)² = x³+x², you mean x³-(x²)



















